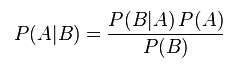忽然想到了一个非常反人类的模型。通常一说到亲属网络,我们一定会想到是一个 tree. 但如果我们用 time series 去想每个人的出生,理论上应该不会有两个人在精确的同一个时间计量时刻上出生,所以每个人的出生可以看成按照 time series 抽了一张卡。假如所有人的出生时刻都是已知的,我们就获得了一个有先后的 chain. 获得了这个模型之后,就可以把这个 chain 上的每一个 nodes/slots 打上特定的标签。譬如打一个是否为「进士」的标签。类比为:有一个全知全能的神在创造人类(抽卡),当前抽卡抽中「进士」(SSR) 卡的概率。于是,1)如果把这个标签换成其他标签,它就是可以用来计算各种主题了 Markov chain 了。2)如果把出生换成其他属性,比如加入到一个 genealogy network 中的时间,我们能对一个特定的家族来计算有趣主题在 time series 上出现的概率。
那么接下来最重要的问题,我们当然无法知道每个人出生的时刻。那么我们可以至少可以把所有已知人物的总数作为生成一些空白 nodes/slots 的数量。接下来,把这些 nodes/slots 连起来获得一个内容为空白的 chain. 接下来我们至少可以用各种方式算出来每一个人在某一个 slot 上的概率。譬如一个儿子出现在父亲出生以前的概率为 0,二女儿比大女儿出生早的概率为 0,两个人在同一个时代出现,那么这两个人出现在这个时代之后 200 年的概率为零等等等。那么我们可以获得一个明确的每个 slots 都有每个人出现概率的 chain 了。如何操作这个 chain 我还不太具备一些知识。但至少用最笨的方法排算排列,用多条 chain 求 expectation,我们仍然能算上一段所比喻的「抽卡问题」下一张卡出现的概率